СТРАНИЦА
РАДОМЫШЕЛЬСКОЙ ЦЕРКВИ ЕВАНГЕЛЬСКИХ ХРИСТИАН-БАПТИСТОВ
|
Наши координаты: | ЗВУК КАК ТАКОВОЙ Вступление Лёгкий удар ложечькой по стакану, и раздаётся мелодичный, постепенно затухающий звон. Это звук рожденный колеблющими стенками стакана.
А что, собственно, представляет собой звук? Ещё в 1807 г. Юнг показал, что звук - это колебания воздуха. Он придумал прибор, с помощью которого смог записать звуковые колебания. Если записать изменения давления воздуха около стенки звенящего стакана, то получится график примерно следующего вида. 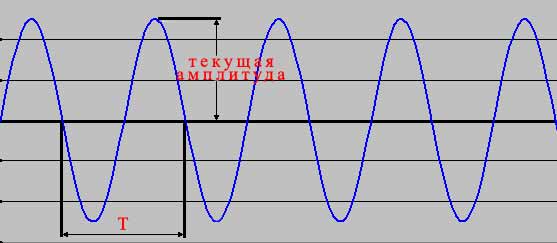 Рассматривая эту кривую, можно обнаружить ряд интересных обстоятельств. Во-первых, колебания давления воздуха ( а следовательно, и колебания частиц ) повторяются через равные промежутки времени, т. е. имеют определённую периодичность. Время, которое продолжается один законченный цикл изменения давления, называют ПЕРИОДОМ повторения, или просто периодом колебаний. Если стенка стакана совершает, например, 800 колебаний в секунду, то один период будет продолжаться 1/ 800 с. ( около 0,0011 с. ). Число колебаний за секунду называют частотой, которую во всём мире измеряют в "герцах". Частоту колебаний в формулах обычно обозначают латинской буквой F, а период колебаний - буквой Т. Таким образом теперь можно составить формулу: T=1/ F или F=1/ T где Т выражено в секундах, а F - в герцах. Вторым обстоятельством, которое бросается в глаза при рассмотрении графика, является то, что размах колебаний постепенно убывает, и это убывание происходит неравномерно: чем дальше, тем медленнее. В технике принято говорить не о размахе, а об амплитуде колебаний. Убывание амплитуды вызвано тем, что энергия, запасённая в стенках стакана в момент удара, постепенно рассеивается в пространстве. В конечном итоге эта энергия превращается в тепло. Звук, издаваемый стаканом, как и большинство звуков в природе, является сложным. Простые звуки представляют собой колебания, описываемые синусоидальным законом. Простой тон можно получить только от камертона или от специальных генераторов, используемых, в частности для наладки радиоаппаратуры. Ом высказал мысль, что наше ухо способно любой сложный звук разлагать на простые тоны и воспринимать их раздельно. В последствии Гельмгольц положил это в основу своей резонансной теории звука. Фурье открыл, что колебания сложной формы можно представить как сумму простых колебаний синусоидальной формы. Эти составляющие сложного колебания называются гармоническими колебаниями ( или коротко - гармониками ). Вообще чем больше инструмент возбуждает гармоник, тем богаче тембр ( окраска звука ) его звучания. Интересным явлением при сложении двух колебаний являются так называемые биения. Биения используют часто для обнаружения небольшой разницы в частотах. Распространяющиеся от точки возникновения простые звуки являются периодически чередующимися зонами сжатого и разряжённого воздуха. Представим распространение простого звука по одному направлению, по одному лучу. Если в некоторый момент времени сразу во многих точках этого луча измерить давление воздуха и результаты измерений представить в форме графика, то получится синусоида. Полный цикл давления называют длинной волны в воздухе (обычно обозначается греческой буквой L ). Если звук имеет частоту F гц., то через любую произвольно взятую, точку пространства возле источника звука за одну секунду пройдёт F волн длинной L м. каждая, а фронт ( передняя граница ) звуковых волн продвинется на расстояние FL. Путь пройденный за одну секунду, есть скорость распространения. Таким образом если обозначить скорость распространения звука в метрах за секунду через V, то V = Fλ или λ= V / F, где λ - в метрах, а частота F - в герцах. Многочисленные измерения показали, что скорость звука в воздухе зависит от его влажности, давления и температуры. При нормальном давлении и температуре скорость звука равна 331 м / с; с повышением температуры и давления она растёт. Человек способен на слух воспринимать звуки разной высоты, но только в пределах определённого слышимого диапазона. Считается что человек может слышать звуки, содержащие частоты в проделах от 16 Гц. до 18 - 19 Кгц. Нижний и особенно верхний предел слышимости частотного диапазона в сильной степени зависят от здоровья и возраста человека. Звуки, имеющие низкую частоту основных колебаний, слышатся как низкие, басовые; звуки с высокой частотой воспринимаются как высокие, тонкие. Помимо высоты тона и тембра каждый звук можно характеризовать силой, которая представляет собой физическую меру интенсивности звука, не зависимую от особенностей слушающего. Не нужно смешивать понятие силы звука с понятием громкости. Громкость - лищ физиологическая оценка звука, связанная с восприятием, а значит, и зависящая от индивидуальных и обще физиологических особенностей нашего слуха. В нотной записи принято указывать на субъективную оценку громкости звука. Градации громкости используют грубые, применяя для обозначения каждой из них итальянские названия: форте - фортиссимо ( fff ) - предельно громко, фортиссимо ( ff ) - очень громко, форте ( f ) - громко, меццо - форте ( mf ) - не очень громко, меццо - пиано ( mp ) - не очень тихо, пиано ( p ) - тихо, пианиссимо ( pp ) - еле слышно. В технике принято говорить не о громкости, а о силе звука, которую определяют величиной амплитуды или величиной уровня звука. Амплитуда измеряется в единицах давления. Уровень показывает во сколько раз одна амплитуда превышает другую, принятую за начальный или нулевой уровень. Если амплитуда какого - либо звука или сигнала меньше этого нулевого уровня, то уровень будет отрицательным, если больше, - положительным. Вернемся к вопросу о давлении. В 1963 г. принята Международная система единиц СИ, в которой давление измеряется в Паскалях, т. е. в ньютонах на один квадратный метр. Наше ухо в состоянии оценивать гигантский диапазон в изменении силы звука ( крайние величины различаются в пять миллионов раз ). За счёт чего же? Оказывается, ухо построено так, что оно реагирует не на изменение силы звука, а примерно на логарифм этого изменения. Измерения показывают: мы обнаруживаем, что сила звука стала иной только в том случае, если изменение амплитуды давления составляет не менее 12%, что соответствует изменению силы звука на 26% ( речь идёт не о простых, а о сложных процентах, поэтому прирост величины изменения идёт сначала медленно, а затем все скорее ). Если воспользоваться этими 12% как ступеньками или шкалы силы звука, начиная от порога слышимости, то до наступления болевого порога уместится примерно 120 делении. Не вдаваясь в детали, укажем только, что токая логарифмическая "ступенька" представляет другую единицу, которая используется в технике и носит название "децибел". Имеется договорённость в международном масштабе принимать за нулевой уровень напряжение равное 0,775 В, и звуковое давление 2*10-5 Па. Структура музыкальных звуков Музыкальный звук несет информацию о своей высоте (то есть о том, какая нота звучит) и тембре или типе музыкального инструмента, с помощью которого производится звукоизвлечение (генерация звука). Кроме того, в структуру музыкального звука исполнитель закладывает свою "импрессию", варьируя силу и резкость начала (атаки) и окончания (затухания), громкость, применяя амплитудное и частотное вибрато. Осциллограмма (график во временной области) типичного сигнала музыкального инструмента показана на рис. 1. 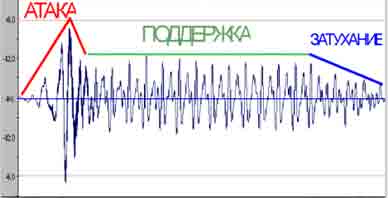 Рис.1. Осциллограмма музыкального звука.
Обычно звук начинается с так называемой атаки, быстрого нарастания амплитуды сигнала. Длительность атаки для разных музыкальных инструментов варьируется от единиц до нескольких десятков или даже сотен миллисекунд. После атаки начинается поддержка, в течение которой уровень сигнала примерно постоянен или плавно меняется в случае применения амплитудного вибрато. По-видимому, во время поддержки формируется ощущение высоты звука. Далее идет участок относительно быстрого затухания, уменьшения величины сигнала. Атака, поддержка и затухание образуют так называемую амплитудную огибающую. Спектр сигнала, то есть представление сигнала в частотной области, показан на рис. 2. 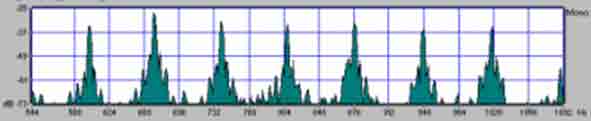 Рис.2. Спектр музыкального звука.
Характерный спектр музыкального сигнала состоит из последовательности (по оси частот) узких "колоколов". Причем частоты, соответствующие максимумам (вершинам) "колоколов", примерно кратны основному тону или "фундаментальной" частоте музыкального звукового сигнала, под которой понимается частота, соответствующая человеческому ощущению высоты звука. Почему я употребил термин узкие "колокола", а не пики, полоски, вертикальные линии и т. п.? Потому, что спектры звуков реальных, "живых", а не синтезированных музыкальных инструментов выглядят именно так. А вот для сигналов, сгенерированных по примитивным алгоритмам "электронными" музыкальными синтезаторами, как раз характерен спектр, состоящий из очень узких вертикальных линий (почти дельта функций). Логично сделать вывод, что чрезмерная узость спектральных линий сигнала таких синтезаторов, возможно, и есть основная причина, приводящая к механистичности, роботоподобности, тусклости и мертвости их звука. Интересно, что, если каким либо образом "размыть" пикоподобные линейчатые спектральные компоненты примитивного сигнала (например, последовательности прямоугольников, меандра), звук станет заметно ярче, живее, теплее. Это можно сделать, например, с помощью программы WaveLab или CoolEdit, добавив амплитудное и частотное вибрато, наложив эффекты "pitch-shift" (небольшое, 0,25-1 Гц смещение частоты основного тона и суммирование с исходным сигналом) и хоруса (небольшое периодическое смещение частоты основного тона за счет периодического плавного изменения задержки сигнала). Теперь о замечании "примерно кратны основному тону". Раньше считалось, что спектр музыкального сигнала состоит из очень узких вертикальных линий, расположенных на частотах F, 2*F, 3*F, ..., где F - первая частотная составляющая спектра, являющаяся также первой гармоникой и фундаментальной частотой (основным тоном) музыкального сигнала. Точные измерения с применением современных методов спектрального анализа сверхвысокого разрешения по методу Прони (это намного точнее БПФ; см. ниже) убедительно доказывают небольшую "не гармоничность" гармоник (координат вершин узких "колоколов" на оси частот) в спектре звука реальных музыкальных инструментов. На самом деле в спектрах реальных сигналов часто отсутствуют несколько первых гармоник, а частоты оставшихся связаны приближенным соотношением примерно такого вида: (3+error1)*F, (4+error2)*F, (5+error3)*F, (6+error4)*F, ..., где F - фундаментальная частота музыкального сигнала, а error1, error2, error3, ... - небольшие случайные величины. Несмотря на то, что фундаментальная частота виртуальна, реально не присутствует в сигнале, это не препятствует возникновению четкого ощущения ее наличия. Такой эффект характерен для звука пианино в субконтроктаве. Да и смоделировать его очень просто. Например, в программе SAW или EDS Tools сгенерируйте сигнал из суммы синусоид с частотами 200 Гц, 250 Гц, 300 Гц, 350 Гц, 400 Гц, 450 Гц и прослушайте его. Еще больше усложняет структуру музыкального сигнала зависимость спектра от амплитудной огибающей. Обычно на стадии атаки количество высокочастотных составляющих максимально и постепенно уменьшается на стадиях поддержки и затухания. Особенно это свойственно звуку пианино и гитары. Хостинг от uCoz
|